[Algorithm] 다익스트라(Dijkstra) 알고리즘

 

 

 

---

다익스트라 알고리즘

 

다익스트라 알고리즘은 1959년 네덜란드의 컴퓨터 과학자 에츠허르 다익스트라가 개발한 최단 경로 탐색 알고리즘이다.

 

 

이 알고리즘은 그래프에서 한 정점에서 다른 모든 정점까지의 최단 거리를 구하는 데 사용되며, 실 생활에 사용되는 예시로는 최단 거리 알고리즘답게 내비게이션 시스템, 네트워크 라우팅 등과 같은 곳에 사용된다.

 

[출처 : https://ko.wikipedia.org/wiki/%EB%8D%B0%EC%9D%B4%ED%81%AC%EC%8A%A4%ED%8A%B8%EB%9D%BC_%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98#]

 

 

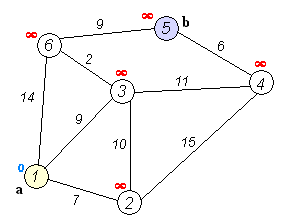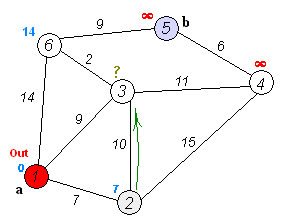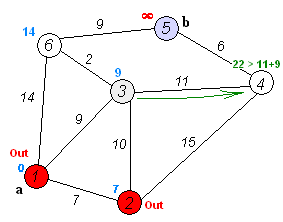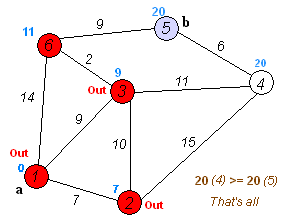
위 예제는 1번 노드(a)에서 5번 노드(b)로 가는 최단 거리를 구하는 과정을 나타낸 것이다.

 

 

기준이 되는 노드에서 방문하지 않은 각 노드 간의 거리를 계산하고, 이를 통하여 가장 낮은 거리로 계산되는 각 노도의 경로를 모두 계산하게 되는 것이다.

 

---

예제

 

아래는 heapq를 활용하여, 위의 예제를 다익스트라 알고리즘을 코드로 구현한 것이다.

 

import heapq

def dijkstra(graph, start):
    distances = {node: float('infinity') for node in graph}
    distances[start] = 0
    queue = [(0, start)]
    visited = set()
    
    while queue:
        current_distance, current_node = heapq.heappop(queue)
        
        if current_node in visited:
            continue
            
        visited.add(current_node)
        
        for neighbor, weight in graph[current_node].items():
            distance = current_distance + weight
            
            if distance < distances[neighbor]:
                distances[neighbor] = distance
                heapq.heappush(queue, (distance, neighbor))
                
    return distances
    
graph = {
    1: { 2:7, 3:9, 6:14 },
    2: { 1:7, 3:10, 4:15 },
    3: { 1:9, 2:10, 4:11, 6:2 },
    4: { 2:15, 3:11, 5:6 },
    5: { 4:6, 6:9 },
    6: { 1:14, 3:2, 5:9 }
}

print(dijkstra(graph,1))

#########################

# 출력 값 : {1: 0, 2: 7, 3: 9, 4: 20, 5: 20, 6: 11}

 

 

 

---